引言
展示实体作为Minecraft的技术性实体之一,它们的作用主要体现在视觉方面。这些实体没有碰撞箱,没有任何自主行为,只能通过技术手段生成。在生成时如果不指定NBT,则不会显示任何内容。原版技术开发者可以用展示实体的常规字段展示一些普通的内容,如正常形状的方块、物品、文字,但如果仅用展示实体展示这些常规内容,未免有些单调。
展示实体的transformation字段是实体格式中较复杂的一个字段,它使用矩阵形式或分解形式来表示展示实体的渲染变换,从而制造一些特殊的效果。
矩阵形式
使用矩阵形式时,字段transformation的数据类型为列表,列表内一共有16个元素,这些元素均为单精度浮点数。这个列表用于表示一个
基础变换形式有平移、旋转、缩放(镜像)、剪切,所有的变换均基于实体的实际坐标进行。
平移
设展示实体上任意一点
则平移矩阵
旋转
一共有三种旋转方式,即绕
于是有
将其转换为仿射矩阵,得到
同理,绕
绕
缩放
设展示实体上任意一点
则缩放矩阵
若
镜像
对于缩放矩阵而言,特别地,若
 \
\
若展示实体上任意一点
其中
剪切
剪切变换将实体上所有点沿某一方向做一定移动,通过原点的直线上任意一点沿该方向移动的距离随直线与原点的距离线性变化,这使得图像变得倾斜。一种剪切变换发生在两个正交坐标轴组成的平面内,在其中一个方向上做剪切,在另一个方向上不做变换。三维坐标系中坐标轴两两正交一共有六对正交关系,因此初等剪切变换一共有六种。
如图,图像在一个方向发生剪切的过程中,实际上与另一个方向拥有一个剪切角度
则
同理可推导得到其他六种剪切变换所需的矩阵。当剪切变换的方向为
以上描述的剪切矩阵均为仅在一个方向上做变换,并与另一个方向呈一定剪切角度的情况。若同时应用多个不同的剪切变换,使用上面的规律填入元素,则剪切矩阵可记为
若某个方向的剪切变换不使用,将矩阵中对应位置的
组合变换
一种变换可能无法满足要求,有时需要同时应用多种以表示复杂的变换。对于有限个仿射变换
注意矩阵的乘法遵循从右向左的运算规则,且不支持交换律,但是支持结合律,因此有
令
在标签transformation中使用的矩阵均为组合变换矩阵。
应用实例
修改一个方块展示实体的NBT数据,使之依次绕
故命令应为
data merge entity @e[type=block_display,limit=1] {transformation:[-0.35f,-0.71f,0.61f,0.0f,0.87f,0.0f,0.5f,0.0f,-0.35f,0.71f,0.61f,0.0f,0.0f,0.0f,0.0f,1.0f]}分解形式
对于这些
式中分块阵
分解形式的transformation字段是分块阵
式中:
称
对上式等号左右两边取转置矩阵,得
由于方阵
对上式进行变形:
方阵
求出
步骤一:
由特征方程
步骤二:
对于每个特征值
步骤三:
如果求得的特征向量相互不正交,则对特征向量
步骤四:
如果求得的向量
对于右奇异向量矩阵
同理可求得右奇异向量矩阵,计算步骤与上述计算左奇异向量矩阵的步骤相同,其中
这样可以不进行对角化计算而直接求出右奇异向量矩阵
矩阵奇异值分解的结果具有几何意义,其中transformation是复合标签:
对于right_rotation和left_rotation这两个字段,有轴角式和四元数形式两种数据形式表示旋转。下面分别介绍这两种数据形式:
轴角式
轴角式旋转可以理解为:一个向量
为了便于分析,将向量
将
于是可得到
对于向量
实际上,在向量
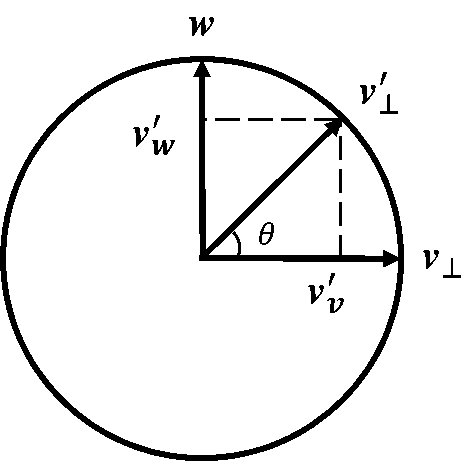
现在考察向量
由
知
所以得到
使用轴角式表示旋转时字段right_rotation和left_rotation为复合标签:
四元数形式
使用四元数形式表示旋转时,字段right_rotation和left_rotation类型是列表,数据格式为:
一切四元数都可以写成如下的形式:
其中
对于轴角式中的旋转轴和向量,可以将其写成纯四元数的形式,如
如果将
注意到,上面的这个四元数q有如下性质:
这是一个单位四元数。一般应用于旋转变换的四元数都是单位四元数,\emphasize{非单位四元数会使得模型在旋转的同时进行缩放}。于是使用四元数形式表示的向量旋转为
令
式中:
于是得到了四元数形式表示的旋转公式:
其中
式中:
对于一个渲染变换,设其初次旋转所用四元数为
进行初次旋转,得到
随后应用缩放变换,得到
在初次旋转和放缩变换共同作用下,模型中各点的相对位置会发生改变。只有当初次旋转四元数
最后应用平移变换,确定模型最终的位置,从而得到点
应用实例
用方块展示实体展示一个玻璃。要求:生成这个展示实体,使玻璃的体对角线与
模型中体对角线从
计算旋转角度:将
旋转轴垂直于旋转前后的向量,有
将其单位化得left_rotation的数据为:
left_rotation:{angle: 54.74f, axis: [-0.71f, 0.0f, 0.71f]}计算再次旋转四元数
模型不需要进行初次旋转、缩放和平移,故transformation字段为:
transformation:{right_rotation: [0.0f, 0.0f, 0.0f, 1.0f], scale: [1.0f, 1.0f, 1.0f], left_rotation: [-0.33f, 0.0f, 0.33f, 0.89f], translation: [1.0f, 1.0f, 1.0f]}生成这个展示实体所需的命令为:
summon block_display ~ ~ ~ {block_state:{Name:"minecraft:glass"},transformation:{right_rotation:[0.0f,0.0f,0.0f,1.0f],scale:[1.0f,1.0f,1.0f],left_rotation:[-0.33f,0.0f,0.33f,0.89f],translation:[1.0f,1.0f,1.0f]}}字段left_rotation的值已定义,旋转动画由插值完成,可由right_rotation定义,待确定的量依然是旋转角度
以right_rotation的数据为
right_rotation: {angle: 90, axis: [0.58f, 0.58f, 0.58f]}转换为四元数形式
right_rotation:[0.41f,0.41f,0.41f,0.71f]同理
right_rotation:[0.58f,0.58f,0.58f,0.0f]}right_rotation:[0.41f,0.41f,0.41f,-0.71f]}right_rotation:[0.0f,0.0f,0.0f,1.0f]}为将模型的旋转角度平滑过渡至
data merge entity @n[type=block_display] {transformation:{right_rotation:[0.41f,0.41f,0.41f,0.71f]},interpolation_duration:20}该命令执行后,应用命令方块电路或函数计划使20gt后、定义的插值动画结束时模型的旋转角度开始平滑过渡至
data merge entity @n[type=block_display] {transformation:{right_rotation:[0.58f,0.58f,0.58f,0.0f]},interpolation_duration:20}20gt后开始平滑过渡至
data merge entity @n[type=block_display] {transformation:{right_rotation:[0.41f,0.41f,0.41f,-0.71f]},interpolation_duration:20}20gt后开始平滑过渡至
data merge entity @n[type=block_display] {transformation:{right_rotation:[0.0f,0.0f,0.0f,1.0f]},interpolation_duration:20}20gt后开始平滑过渡至data\minecraft\function\animation下创建90.mcfunction、180.mcfunction、270.mcfunction、0.mcfunction四个函数。例如,函数90.mcfunction的内容可以如下所示:
data merge entity @n[type=block_display] {transformation:{right_rotation:[0.41f,0.41f,0.41f,0.71f]},interpolation_duration:20}
schedule function minecraft:animation/180 20t参考文献
[1] https://zh.minecraft.wiki/w/展示实体
[2] https://krasjet.github.io/quaternion/quaternion.pdf
[3] https://blog.csdn.net/YiYeZhiNian/article/details/106750302
[4] https://zhuanlan.zhihu.com/p/45404840
[5] https://zhuanlan.zhihu.com/p/183973440